Bezier Curves for Smooth Freehand Drawing on Canvas

Introduction

Today's article will cover:

• Principles of Bezier curves, control points, curve equations, and the derivation and implementation of quadratic and cubic Bezier curves
• Implementation of freehand brush
• Optimizing writing with Bezier curves

Curve Equation

A curve equation is a mathematical expression used to describe the shape of a curve in a plane or three-dimensional space. It can include various types of curves such as arcs, circles, ellipses, parabolas, hyperbolas, etc.

Drawing a curve involves calculating a series of points based on the curve equation and then connecting these points.

Curve equations can be represented in different ways, such as Cartesian equations, parametric equations, polar coordinates, etc.

For example, the circle we learned in high school can be represented using the x and y coordinates in the Cartesian coordinate system to describe the geometric properties of a circle.

x^2 + y^2 = r^2

In this equation, (x, y) represents any point on the plane, and r is the radius of the circle. This equation describes the geometric properties of a circle with radius r centered at the origin (0, 0).

A circle can also be represented using parametric equations:

x(t) = r * cos(t)
y(t) = r * sin(t)

Here, (x(t), y(t)) represents the coordinates of a point on the circle, r is the radius of the circle, and t is the parameter, usually varying between 0 and 2π (one complete revolution). This parametric equation describes how the points on the circle change with the parameter t and radius r.

Bezier Curves

Bezier curves are a type of mathematical curve introduced by French engineer Pierre Bézier in the first half of the 20th century.

They solve the following problems:

• Curve modeling and control: Bezier curves solve the problem of smooth curve modeling and control. They allow users to easily create smooth curves, paths, and shapes, and precisely control the shape of the curves by adjusting the positions of the control points.
• Animation paths: Bezier curves are used as animation paths, allowing objects to move along smooth trajectories and creating smooth animation effects.
• Data interpolation: Bezier curves can be used to connect data points with curves for data visualization and mathematical modeling.

In summary, compared to specific shape curve equations, the success of Bezier curves lies in providing a universal, definable, precise, and flexible way to describe irregular curves.

The generation of Bezier curves is determined by two parts:

• Anchor points: start point and end point (sometimes referred to as control points together with anchor points; in this article, we use them separately)
• Control points

For example, to draw a curve between points A and C, we can choose point B between the anchor points A and C as a control point, and then draw the curve ABC.

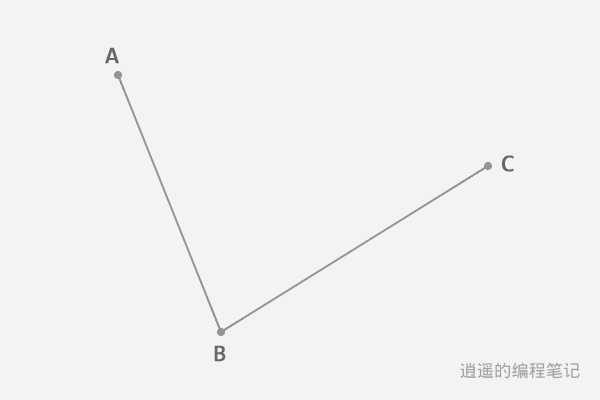
You can think of B as a pulling point that will bend the original line segment AC into a curve.

Complete demo 👉 Online Preview, view the example code here

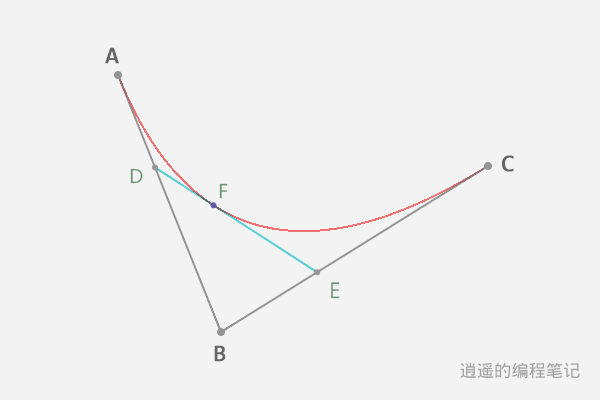
There can be multiple control points, for example, we can choose points B and C between points A and D as control points, and then draw the curve ABCD.

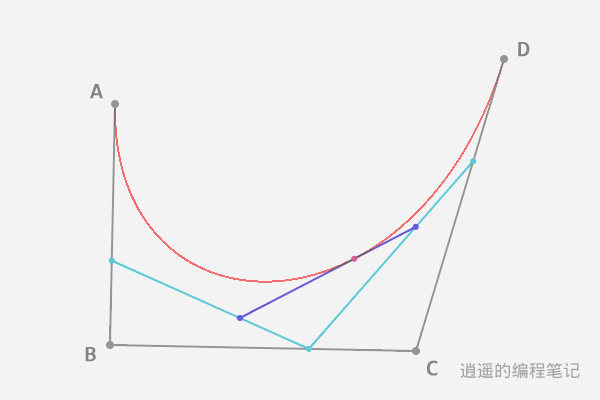
The number of control points determines the degree of the Bezier curve.

• A Bezier curve with 0 control points is called a linear Bezier curve.
• A Bezier curve with 1 control point is called a quadratic Bezier curve.
• A Bezier curve with 2 control points is called a cubic Bezier curve.

Linear Bezier Curve

To understand linear Bezier curves, we need to first understand the concept of linear interpolation.

In Bezier curves, linear interpolation can be used to calculate any point between the start and end points on the curve.

The principle of linear interpolation is to calculate a point B on the curve between the start and end points based on the value of the parameter t (usually between 0 and 1) using the following formula:

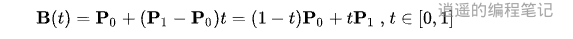
Here, B(t) is a point on the curve, P0 is the start point, P1 is the end point, P1-P0 represents the distance between them, and t is a parameter between 0 and 1.

The code can be represented as follows:

function lerp(start, end, t) {
  return start + (end - start) * t
}

Using the lerp function, we can easily draw a linear Bezier curve.

function renderPoint(x, y, r) {
  ctx.beginPath()
  ctx.arc(x, y, r, 0, 2 * Math.PI)
  ctx.fill()
  ctx.closePath()
}
function renderScene() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.fillStyle = 'black'
  ctx.fillRect(0, 0, canvas.width, canvas.height)
  ctx.fillStyle = 'white'
  for (let t = 0; t <= 1; t += 0.05) {
    let x = lerp(p0.x, p1.x, t)
    let y = lerp(p0.y, p1.y, t)
    renderPoint(x, y, 2)
  }
}

renderScene()

When we change t += 0.05 to t += 0.01, we can see a smoother curve.

Complete demo 👉 Online Preview, view the example code here

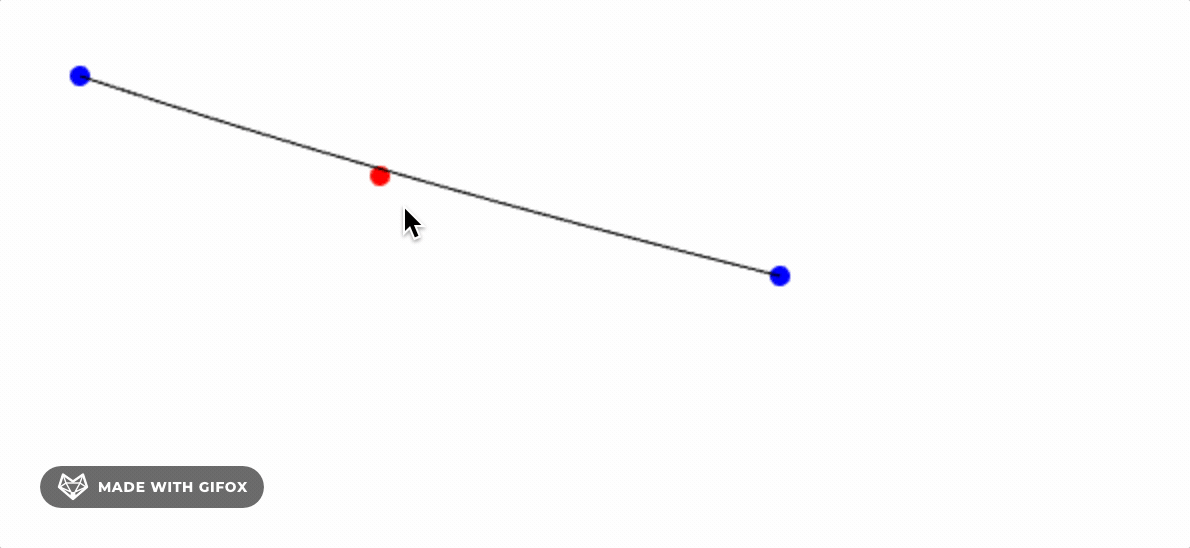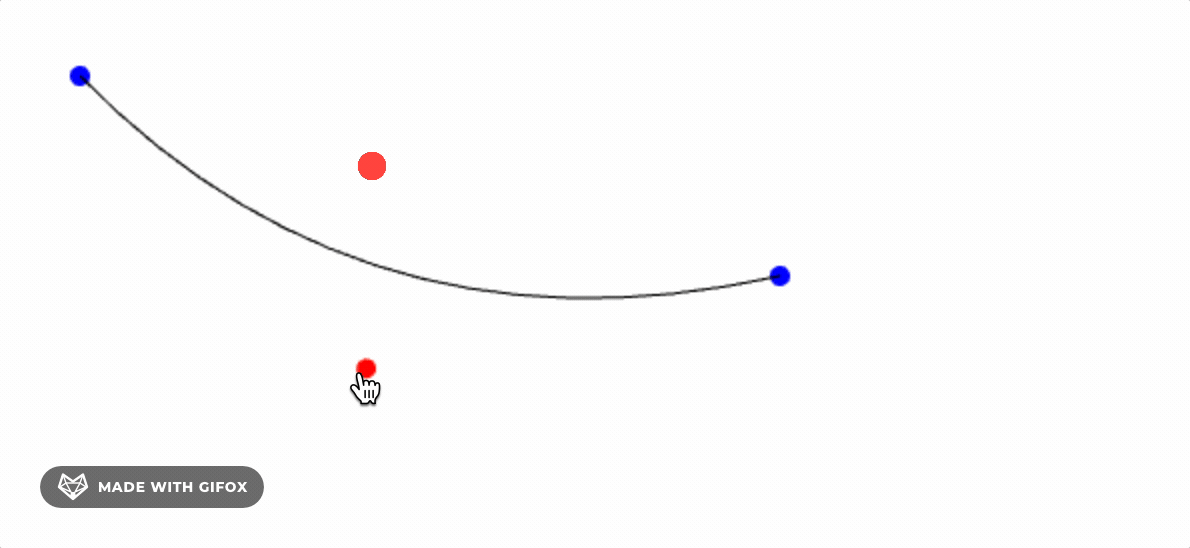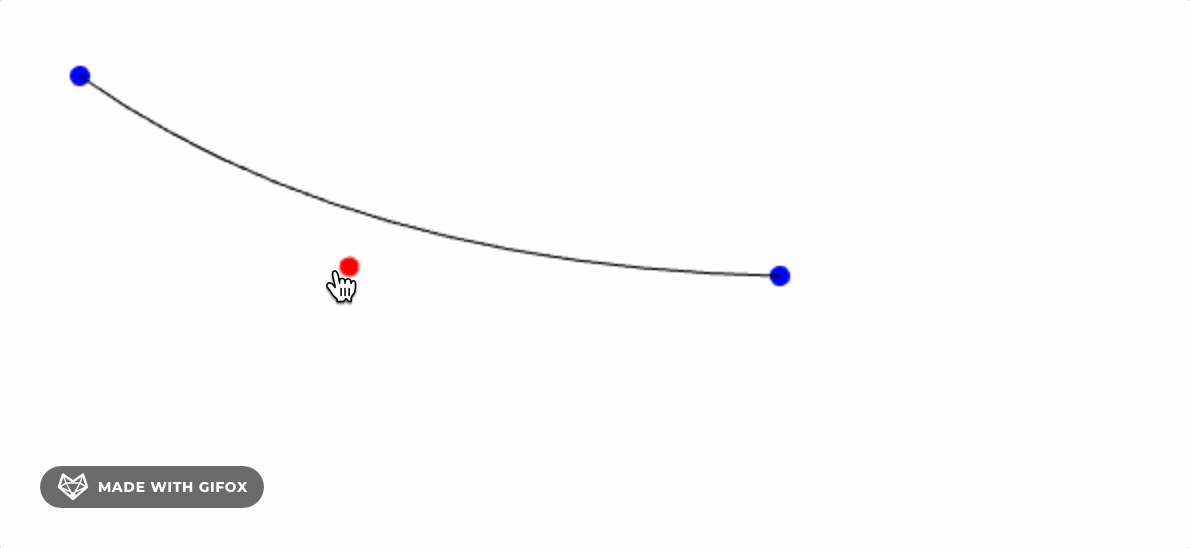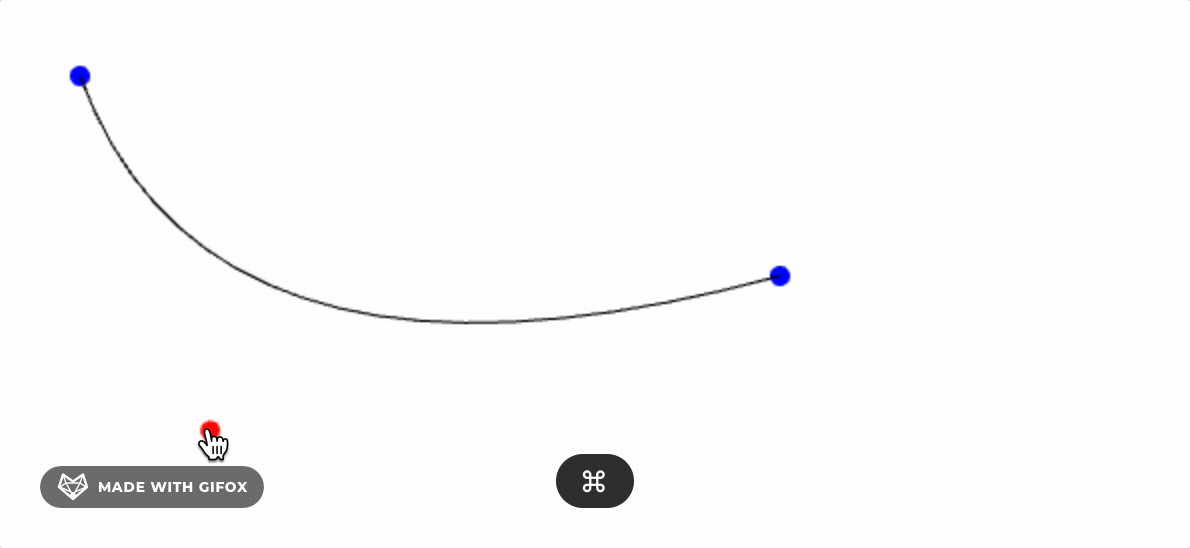
Quadratic Bezier Curve

For a quadratic Bezier curve, we need three points: the start point p0, the control point p1, and the end point p2.

We use linear interpolation to calculate the point B1 between p0 and p1, and the point B2 between p1 and p2, and then calculate the point B between B1 and B2.

Where:

B1 = p0 + (p1 - p0) * t
B2 = p1 + (p2 - p1) * t
B = B1 + (B2 - B1) * t = p0 + (p1 - p0) * t + (p1 + (p2 - p1) * t - (p0 + (p1 - p0) * t)) * t

The expanded polynomial is as follows: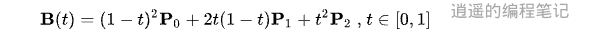

Using the lerp function in the formula, we get:

B1 = lerp(p0, p1, t)
B2 = lerp(p1, p2, t)
B = lerp(B1, B2, t) = lerp(lerp(p0, p1, t), lerp(p1, p2, t), t)

Let's slightly modify the previous example.

function renderScene(step) {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.fillStyle = 'black'
  ctx.fillRect(0, 0, canvas.width, canvas.height)
  ctx.fillStyle = 'white'
  for (let t = 0; t <= 1; t += step) {
    const x1 = lerp(p0.x, p1.x, t)
    const y1 = lerp(p0.y, p1.y, t)
    const x2 = lerp(p1.x, p2.x, t)
    const y2 = lerp(p1.y, p2.y, t)
    const x = lerp(x1, x2, t)
    const y = lerp(y1, y2, t)
    renderPoint(x, y, 2)
  }
}

By adding mouse events to change the position of the control point, we can see the quadratic Bezier curve.

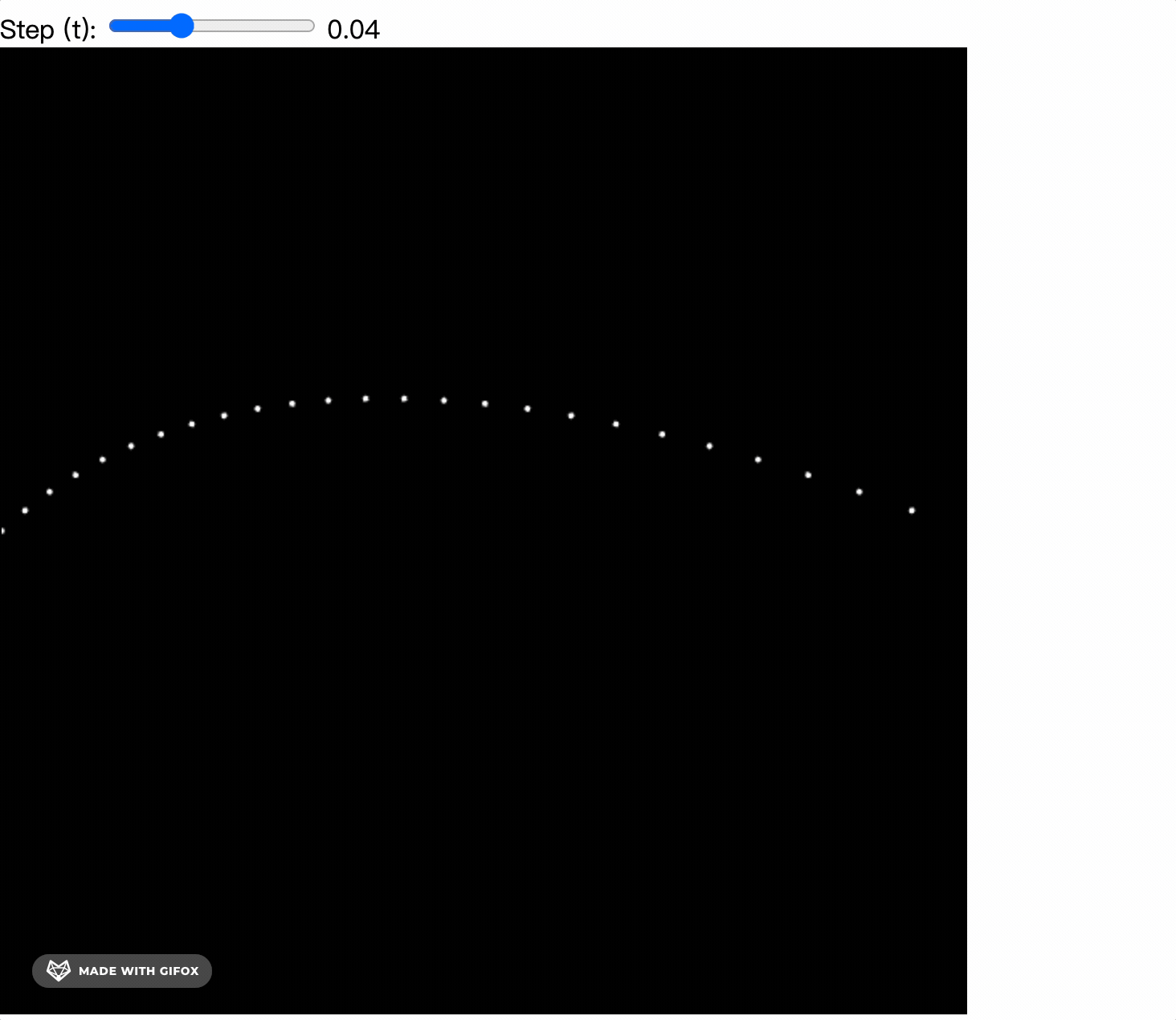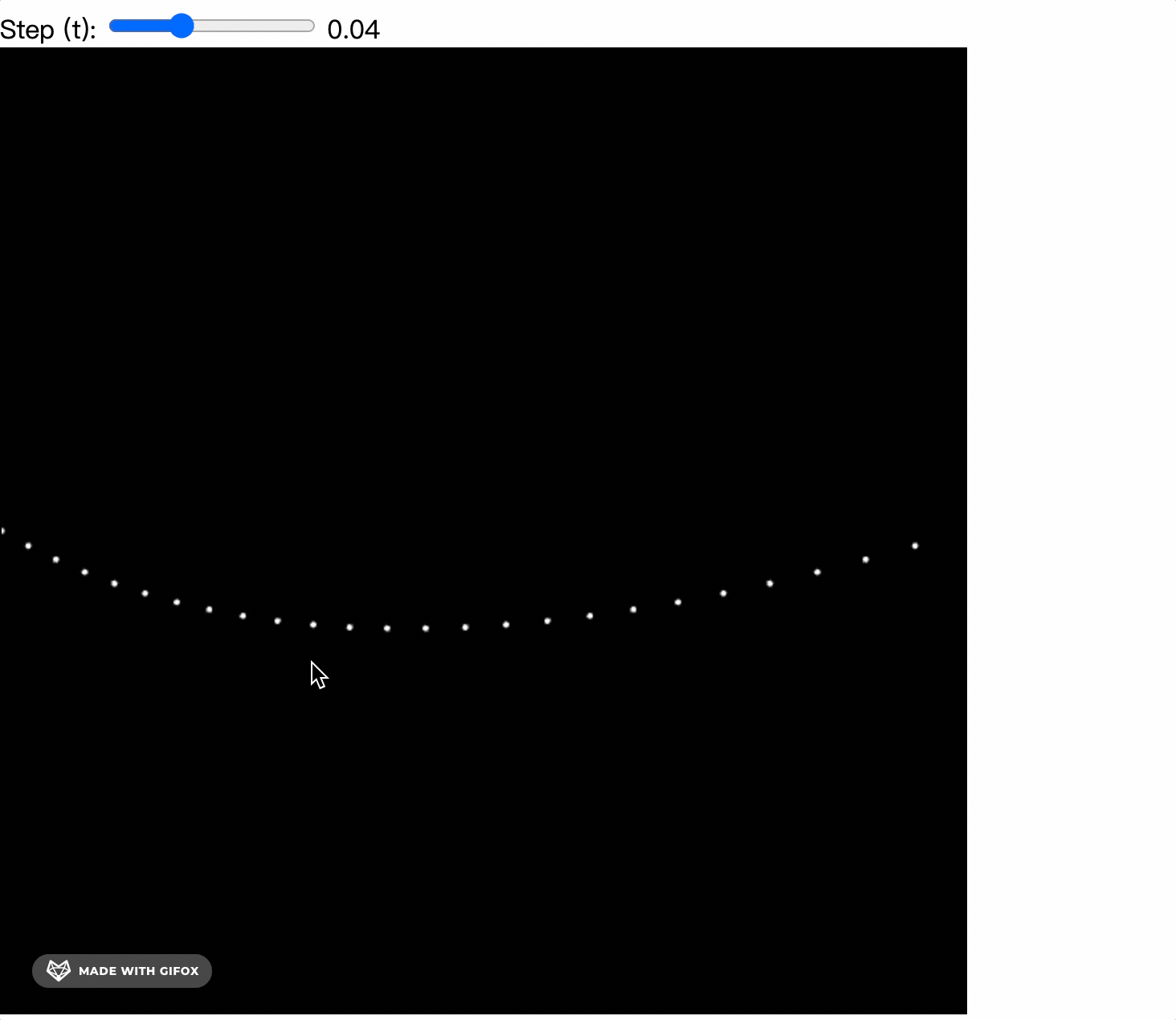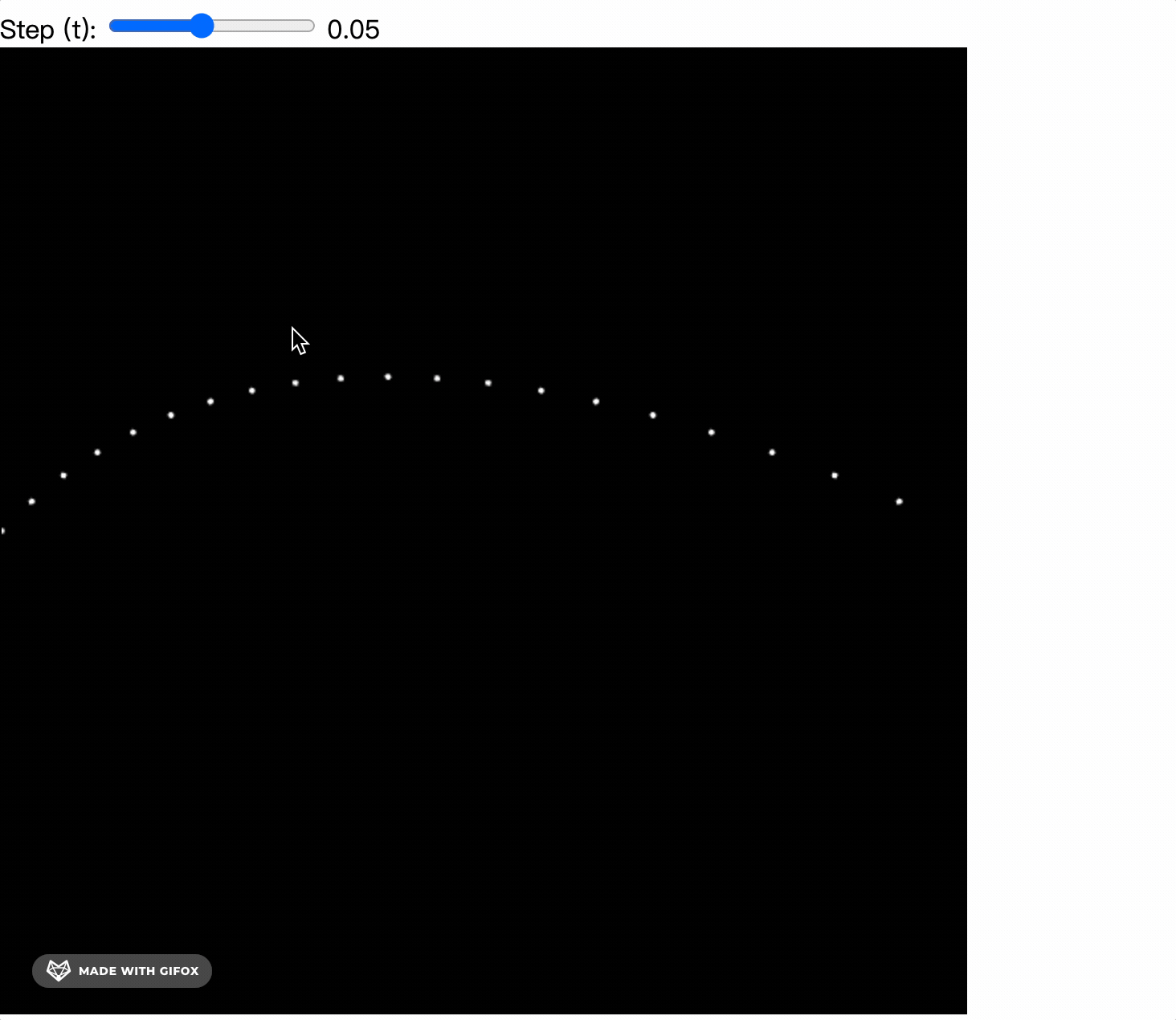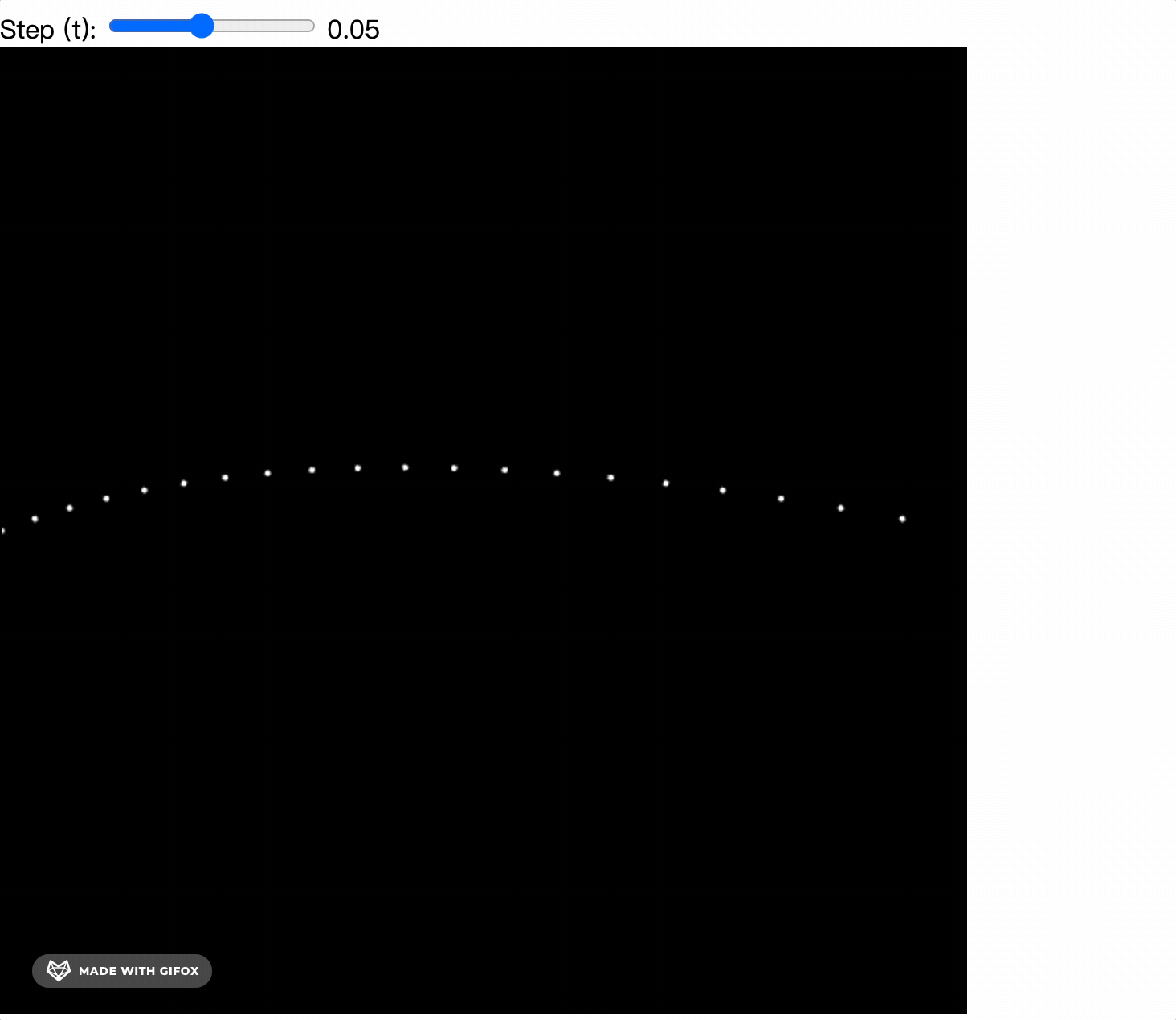
The key point is, if we connect B1 and B2 during rendering, we can see the magical grid.

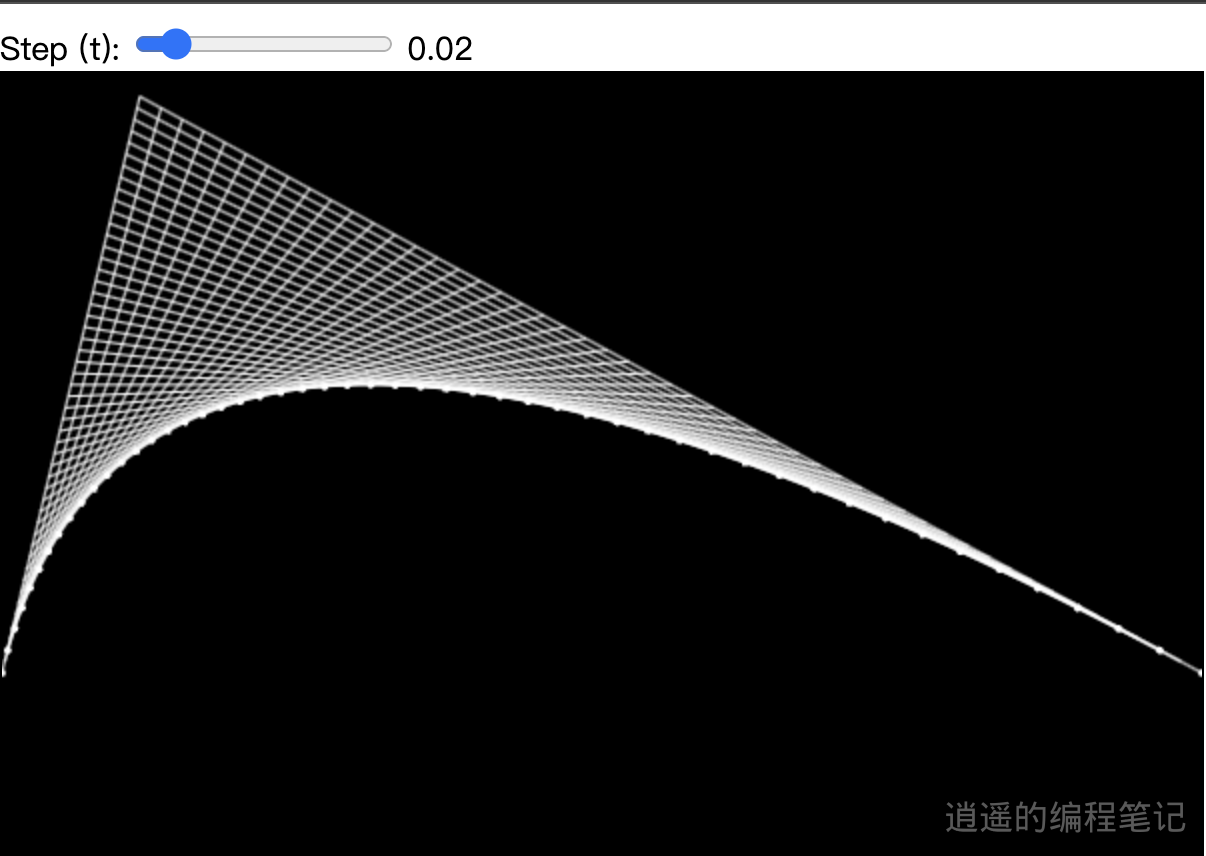
Complete demo 👉 Online Preview, view the example code here

Cubic Bezier Curve

For a cubic Bezier curve, we follow a similar method. We need four points: the start point p0, control points p1 and p2, and the end point p3.

We need to perform interpolation again on the basis of the quadratic curve. To simplify the code, we first abstract the quadratic function.

function quadratic(p0, p1, p2, t) {
  const x1 = lerp(p0.x, p1.x, t)
  const y1 = lerp(p0.y, p1.y, t)
  const x2 = lerp(p1.x, p2.x, t)
  const y2 = lerp(p1.y, p2.y, t)
  const x = lerp(x1, x2, t)
  const y = lerp(y1, y2, t)
  return { x, y }
}

The final implementation looks like this.

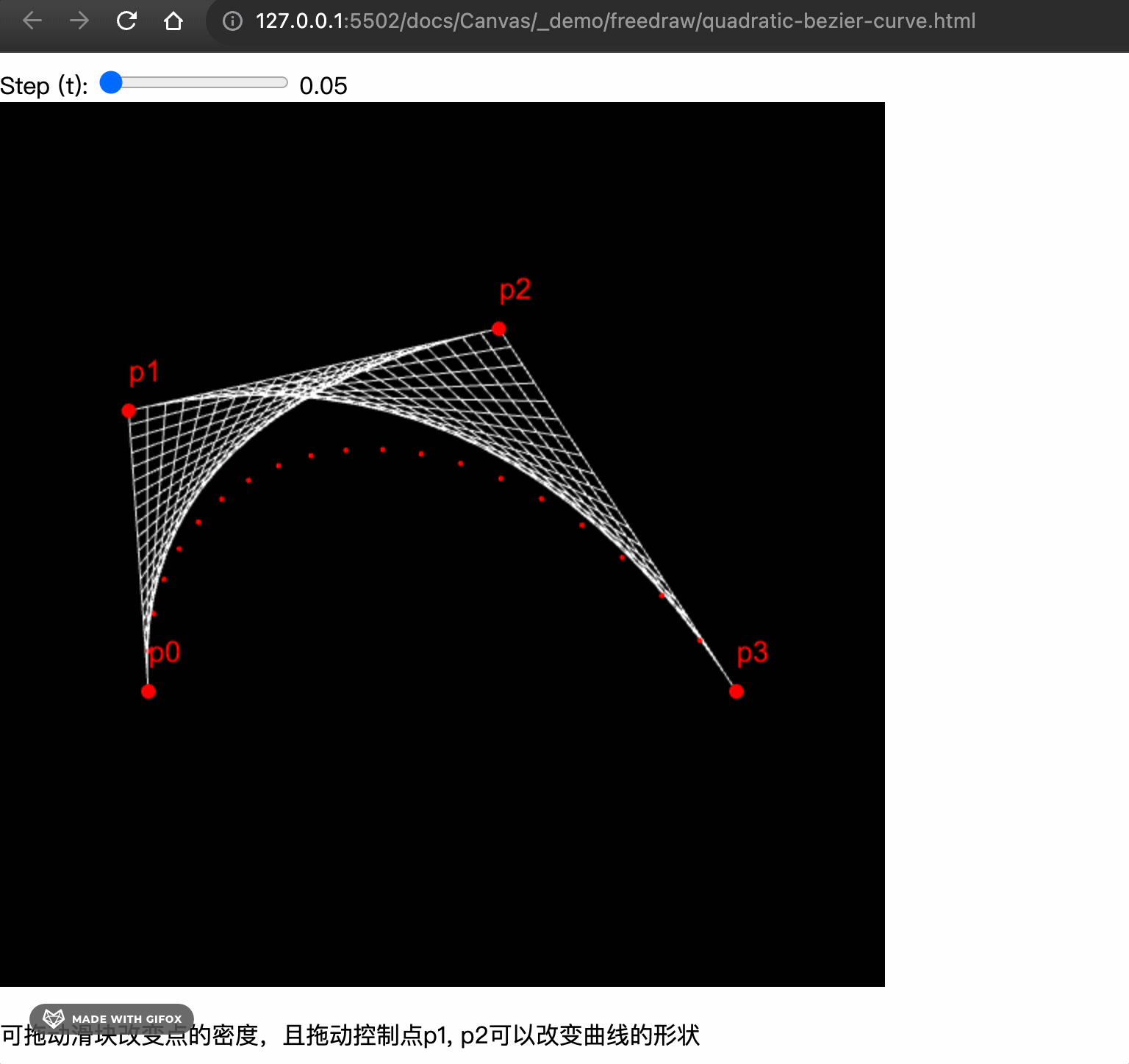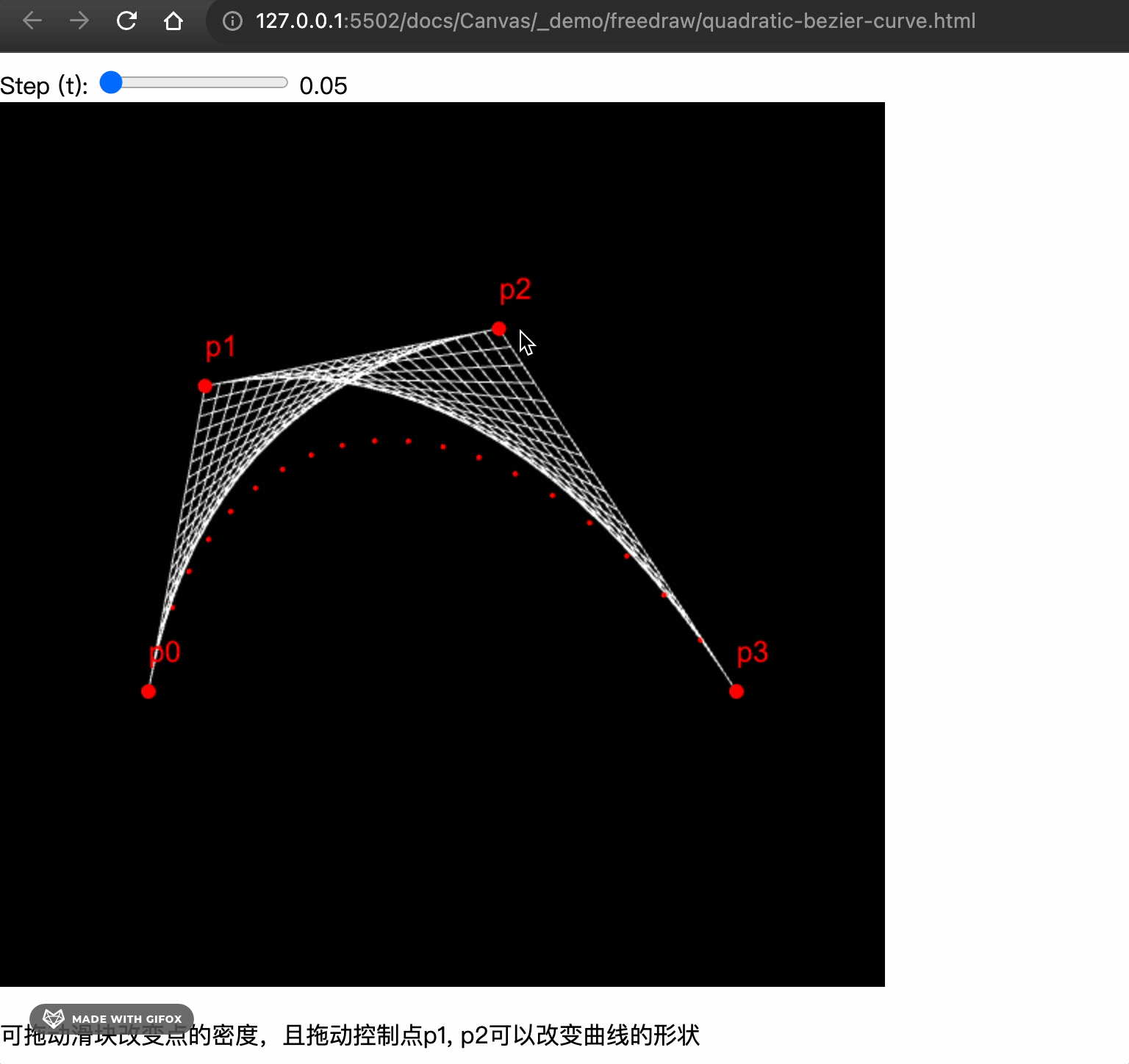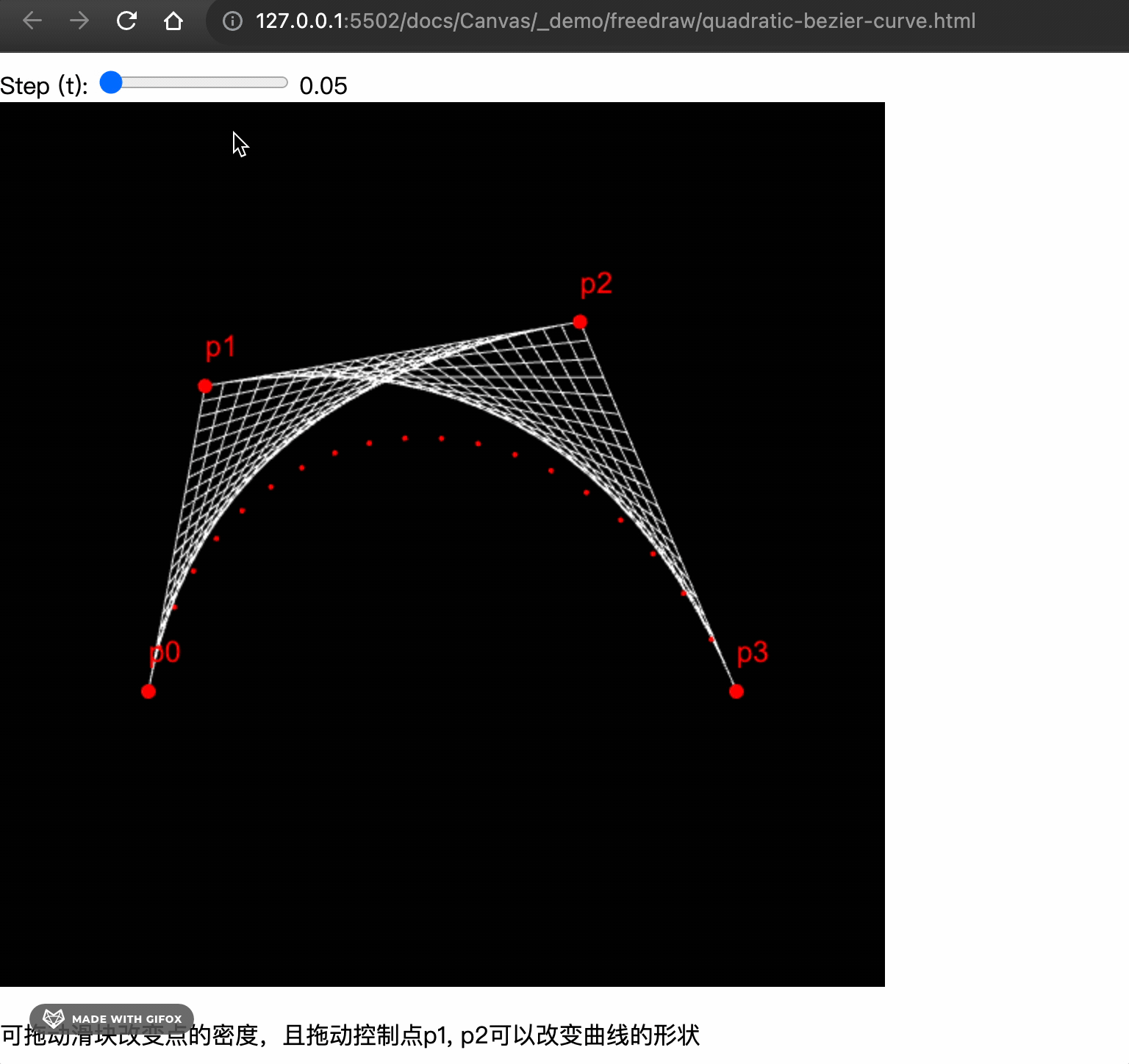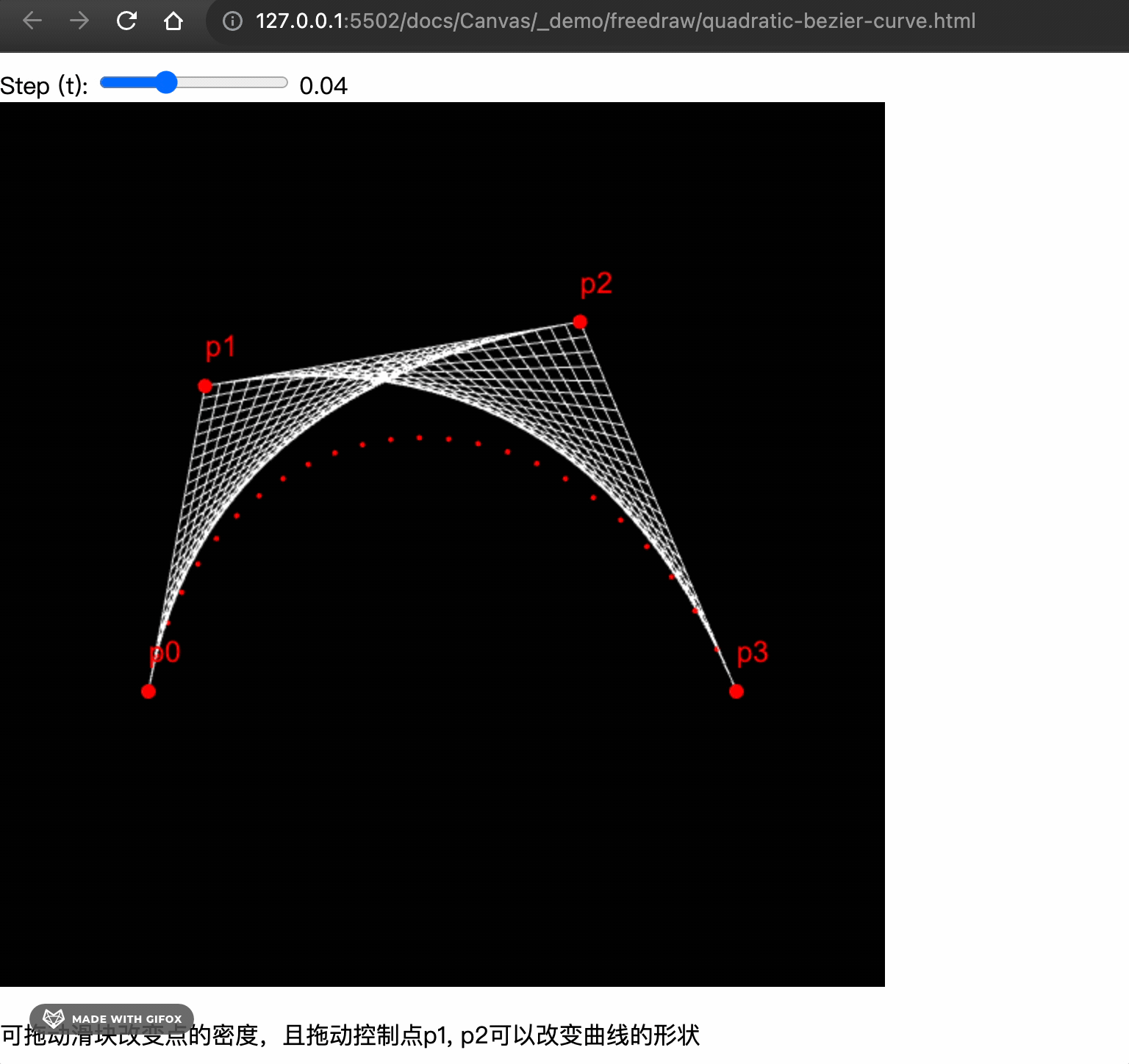
Complete demo 👉 Online Preview, view the example code here

We can extract a corresponding cubic function.

function cubic(p0, p1, p2, p3, t) {
  const v1 = quadratic(p0, p1, p2, t)
  const v2 = quadratic(p1, p2, p3, t)
  const x = lerp(v1.x, v2.x, t)
  const y = lerp(v1.y, v2.y, t)
  return { x, y }
}

The corresponding modification of renderScene is as follows.

for (let t = 0; t <= 1.0000001; t += step) {
  const { x, y } = cubic(p0, p1, p2, p3, t)
  renderPoint(x, y, 2)
}

The expanded formula is as follows: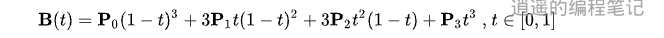

Implementation of Freehand Brush

The principle of the freehand brush: listen to mouse events, record the trajectory of the mouse movement, and then connect these points to form a line, achieving the effect of a freehand brush.

drawingCanvas.addEventListener('pointerdown', (e) => {
  updatePointCounter(0)
  drawing = true
  points = []
  addPoint(e)
})

drawingCanvas.addEventListener('pointermove', (e) => {
  if (drawing) {
    addPoint(e)
    renderFreedraw(drawingCtx, points)
  }
})

drawingCanvas.addEventListener('pointerup', () => {
  drawing = false
  createElement(points)
})

The method to render the freehand path simply calls ctx.lineTo to connect all the points.

function renderFreedraw(ctx, points) {
  ctx.strokeStyle = 'black'
  ctx.lineWidth = 20
  ctx.lineJoin = 'round'
  ctx.lineCap = 'round'
  ctx.beginPath()
  for (let i = 0; i < points.length; i++) {
    const { x, y } = points[i]
    if (i === 0) {
      ctx.moveTo(x, y)
    } else {
      ctx.lineTo(x, y)
    }
  }
  ctx.stroke()
}

Complete demo 👉 Online Preview, view the example code here

Note: The example uses two layers of canvases to optimize performance, avoiding repeated drawing of existing but unchanged graphics.

Optimizing Writing with Bezier Curves

The previous method relies on the density of point collection, which has relatively low performance. Another approach uses fewer points and leverages Bezier curves for smoothing.

Leaving the rest of the code unchanged, we need to modify the rendering method to use Bezier curves.

function renderFreedraw(ctx, points) {
  if (points.length < 2) {
    return
  }
  ctx.strokeStyle = 'black'
  ctx.lineWidth = 20
  ctx.lineJoin = 'round'
  ctx.lineCap = 'round'

  ctx.beginPath()
  ctx.moveTo(points[0].x, points[0].y)

  for (let i = 1; i < points.length; i++) {
    // Calculate control point, taking the midpoint of two points as the control point
    const xc = (points[i].x + points[i - 1].x) / 2
    const yc = (points[i].y + points[i - 1].y) / 2
    // Call the Bezier curve method
    ctx.quadraticCurveTo(points[i - 1].x, points[i - 1].y, xc, yc)
  }

  ctx.stroke()
}

You can see that the curve fitted by Bezier curves is smoother.

Complete demo 👉 Online Preview, view the example code here

Choosing the midpoint of two points as the control point is often used to create smooth curves. This method ensures the curve passes through the two points and has a smooth corner between them. The principle is that the tangent of the curve at the control point is parallel to the tangent of the curve at the midpoint of the two points, making the curve transition smoother.

References

• bezierinfo - Comprehensive Bezier Curve Introduction Tutorial

• Wikipedia Bézier_curve

• MDN cubic-bezier_function